ワールド座標系の基礎 1
この記事では, ワールド座標系について解説します. 仕事で扱うことがあるので理解を深めるためにまとめてみました.
画像の幾何学的モデル
ここでは, 理想的な条件においてモデルの概念説明を行う.
ピンホールカメラモデル
ピンホール位置(光学中心)を原点とする3次元空間の座標を ,
の平面を投影面, 投影面上の画像中心を原点とする座標画像を
とする.

この時, 物体の高さ と投影面上にできる画像の大きさ
との関係は,
である. 同様に考えると,
は
$$x=-f\frac{X}{Z}$$
$$y=-f\frac{Y}{Z}$$
となる.
透視投影モデル
ピンホールモデルの場合, 上下左右反転となるため取り扱いが煩わしいため, コンピュータービジョンでは透視投影モデルを利用する. 透視投影モデルでは, 光学中心よりも後方のピンホールで反転した像を取り扱うのではなく, 光学中心よりも焦点距離分だけ物体側に仮想投影面を置き, そこに反転していない像を描画するモデルである.

前述の定義より自明であるが, は
$$x=f\frac{X}{Z}$$
$$y=f\frac{Y}{Z}$$
となる.
画像と空間の幾何学的関係
座標系 (CS; coordinate system) 概要
| 名称 | 概要 |
|---|---|
| 画像座標系 (image CS) | ピクセル単位のカメラ画像 |
| 正規化画像座標系 (normalized image CS) | その名の通り, 画像座標系(pixel単位, 画像左上が原点)を正規化して実距離空間で扱えるようにした座標系(mm単位, 画像の中心が原点). 正規化の際に, レンズ光軸と画像座標系中心のずれ, 座標原点の変換, 仮想平面への距離を |
| カメラ座標系 (camera CS) | カメラの光学中心を原点とし, Z軸をカメラの光軸方向に一致させ, X軸とY軸は画像の横方向と縦方向に平行にとった座標系. |
| ワールド座標系 (world CS) | カメラ座標とは独立の任意の座標系. |
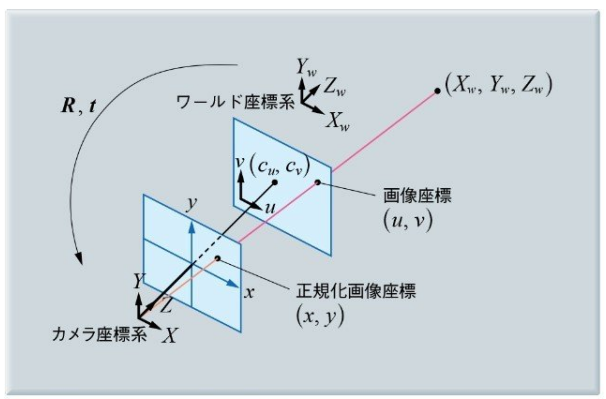
絵の説明:
- 正規化画像座標系は
- カメラ座標系の Z 軸と画像中心が一致する.
- 焦点距離は
が仮定されている.
- カメラ座標系の Z 軸と画像座標系の中心は一致しない(カメラ中心と光学中心はずれている)
正規化画像座標系とワールド座標の関係式
正規化画像座標系とカメラ座標の関係
カメラ座標系の空間位置 と正規化画像上の位置
には, 以下の関係が成り立つ. これは, ピンホールカメラモデルと透視投影モデルの組み合わせである.
$$x = \frac{X}{Z}$$
$$y = \frac{Y}{Z}$$
カメラ座標系とワールド座標系の関係
空間中のある任意な位置に任意の方向で存在するワールド座標系を考える. ワールド座標系における任意の空間の点を とし, 同じ点をカメラ座標系で表した位置
との関係を定式化すると,
$$ \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} = \boldsymbol{R} \begin{pmatrix} X_w \\ Y_w \\ Z_w \end{pmatrix} + \boldsymbol{t} $$
ここで, ,
はワールド座標系を画像座標系に変換する回転行列(3x3)と平行移動ベクトル(カメラ座標から見たワールド座標系原点の位置)である.
$$ \boldsymbol{R} = \begin{pmatrix} r_{11} & r_{12} &r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{pmatrix} $$ $$ \boldsymbol{t} = \begin{pmatrix} t_1 \\ t_2 \\ t_3 \end{pmatrix} $$
回転行列について: 回転の順序によりマトリックスが異なる点に注意.
ここでは, ある点が 軸周りに角度
,
軸周りに角度
,
軸周りに角度
と, 順に回転する場合を考える. 回転行列は,
$$ \begin{align} \boldsymbol{R} &= \boldsymbol{R_Z} \cdot \boldsymbol{R_Y} \cdot \boldsymbol{R_X} \\ &= \begin{pmatrix} \cos{\gamma} &-\sin{\gamma} &0 \\ \sin{\gamma} &\cos{\gamma} &0\\ 0 &0 &1 \end{pmatrix} \begin{pmatrix} \cos{\beta} &0 &\sin{\beta} \\ 0 &1 &0\\ -\sin{\beta} &0 &\cos{\beta} \end{pmatrix} \begin{pmatrix} 1 &0 &0 \\ 0 &\cos{\alpha} &-\sin{\alpha}\\ 0 &\sin{\alpha} &\cos{\alpha} \end{pmatrix} \\ &= \begin{pmatrix} cos{\beta}\cos{\gamma} &-\cos{\alpha}\sin{\gamma}+\sin{\alpha}\sin{\beta}\cos{\gamma} &\sin{\alpha}\sin{\gamma}+\cos{\alpha}\sin{\beta}\cos{\gamma} \\ \cos{\beta}\sin{\gamma} &\cos{\alpha}\cos{\gamma}+\sin{\alpha}\sin{\beta}\sin{\gamma} &-\sin{\alpha}\cos{\gamma}+\cos{\alpha}\sin{\beta}\sin{\gamma}\\ \sin{\beta} &\sin{\alpha}\cos{\beta} &\cos{\alpha}\cos{\beta} \end{pmatrix} \end{align} $$
画像座標系と正規化画像座標の関係
画像座標を とする. 正規化画像座標は, これまでの説明通り
とする.
画像座標系と正規化画像を紐づける以下のパラメータを定義する.
| パラメータ名 | 記号 | 単位 |
|---|---|---|
| カメラ焦点距離 | |
mm |
| カメラ画素横方向サイズ | |
mm |
| カメラ画素縦方向サイズ | |
mm |
| 画像座標系における光軸と画像面(投影面)との交点の横方向位置 | |
pixel |
| 画像座標系における光軸と画像面(投影面)との交点の縦方向位置 | |
pixel |
- 画像座標系における光軸と画像面(投影面)との交点を画像中心と呼ぶ.
- CCD の物理的な配置により, 光軸との交点が必ずしも CCD の中心と一致しないため, ここでいう画像中心は, 入力画像の中心に位置するとは限らない.
- 厳密には CCD と光軸が完全には直交しないが, 無視できるほど小さいとみなす.
上記パラメータを使って画像座標系と正規化画像座標系の関係式を表すと, $$x=\frac{\delta_u(u-c_u)}{f}$$ $$y=\frac{\delta_v(v-c_v)}{f}$$