二次元座標の基本的な座標変換（拡大/縮小/回転/鏡像/スキュー）は, ベクトルと行列を用いて $$\boldsymbol{x'}=\boldsymbol{A}\boldsymbol{x}$$ と表現される. ここで, $$ \boldsymbol{x}= \begin{pmatrix} x \\ y \end{pmatrix} , \boldsymbol{x'}= \begin{pmatrix} x' \\ y' \end{pmatrix} , \boldsymbol{A}= \begin{pmatrix} a & b \\ c & d \end{pmatrix} $$ である.

平行移動を考える

非常に簡単な以下の式で表現できる. $$x' = x + t_x$$ $$y'= y + t_y$$ 数式自体は非常に単純であるが, 前節で定義したベクトルと行列を用いた形式では表現は不可能で, 行列の掛け算で表現できなくなり取り扱いが面倒である.

=>　同次座標系を用いてベクトル演算で記述できるようにすると便利 !!

同次座標

簡単のため 2 次元座標系で説明する. 座標 $(x,y)$ に対して, 要素数を 1 つ増やした座標 $(\xi_1,\xi_2,\xi_3)$ を以下の関係式を満たすように定義する. ただし, 少なくとも一つの要素は 0 ではないものとする. しばしば, $\xi_3=1$ が選ばれる. $$x=\frac{\xi_1}{\xi_3}$$ $$y=\frac{\xi_2}{\xi_3}$$

例: $$(x,y) = (1,2)$$ $$(\xi_1,\xi_2,\xi_3) = (1,2,1)$$

元々の座標系に戻す際, 定数倍した座標（同値関係）も同じ座標となる.

座標系変換の同次座標による記述

平行移動

$$ \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} \sim \begin{pmatrix} 1 &0 &t_x \\ 0 &1 &t_y \\ 0 &0 &1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} $$

線形変換

$$ \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} \sim \begin{pmatrix} a &b &0 \\ c &d &0 \\ 0 &0 &1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} $$

アフィン変換 (affine transformation)

任意の線形変換と平行移動を組み合わせた変換. 変換行列は, 平行移動と線形変換の合成変換となる.

$$ \begin{align} \begin{pmatrix} 1 &0 &t_x \\ 0 &1 &t_y \\ 0 &0 &1 \end{pmatrix} \begin{pmatrix} a &b &0 \\ c &d &0 \\ 0 &0 &1 \end{pmatrix} &= \begin{pmatrix} a &b &t_x \\ c &d &t_y \\ 0 &0 &1 \end{pmatrix} \end{align} $$

射影変換 (projective transformation)

アフィン変換よりも一般化された表現. $$ \tilde{\boldsymbol{x'}} \sim \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} , \tilde{\boldsymbol{x}} \sim \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} , \boldsymbol{H} \sim \begin{pmatrix} h_{11} &h_{12} &h_{13} \\ h_{21} &h_{22} &h_{23} \\ h_{31} &h_{32} &h_{33} \end{pmatrix} $$

を用いて,

$$\tilde{\boldsymbol{x'}} \sim \boldsymbol{H} \tilde{\boldsymbol{x}} $$ と定義される. 座標 $(x', y')$ は同次座標の定義より

$$ x' = \frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}} $$ $$ y' = \frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}} $$

となる.

同次座標によるワールド座標の表現

これまでの説明で述べた通り, 正規化画像座標, 画像座標, カメラ座標, ワールド座標はそれぞれ $$ \boldsymbol{x}= \begin{pmatrix} x \\ y \end{pmatrix} , \boldsymbol{m}= \begin{pmatrix} u \\ v \end{pmatrix} , \boldsymbol{X}= \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} , \boldsymbol{X_w}= \begin{pmatrix} X_w \\ Y_w \\ Z_w \end{pmatrix} $$

であるとする. これらの座標の同次座標表現はそれぞれ, $$ \tilde{\boldsymbol{x}} \sim \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} , \tilde{\boldsymbol{m}} \sim \begin{pmatrix} u \\ v \\ 1 \end{pmatrix} , \tilde{\boldsymbol{X}} \sim \begin{pmatrix} X \\ Y \\ Z \\ 1 \end{pmatrix} , \tilde{\boldsymbol{X_w}} \sim \begin{pmatrix} X_w \\ Y_w \\ Z_w \\1 \end{pmatrix} $$ となる.

正規化画像座標系とカメラ画像系の関係

前述の,

$$x = \frac{X}{Z}$$ $$y = \frac{Y}{Z}$$ を同次座標で表現すると, $$ \begin{align} \tilde{\boldsymbol{x}} \sim \begin{pmatrix} 1 &0 &0 &0 \\ 0 &1 &0 &0 \\ 0 &0 &1 &0 \end{pmatrix} \begin{pmatrix} X \\ Y \\ Z \\ 1 \end{pmatrix} &= (\boldsymbol{I} | 0)\tilde{\boldsymbol{X}} \end{align} $$

カメラ座標系とワールド座標系の関係

前述の, $$ \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} = \boldsymbol{R} \begin{pmatrix} X_w \\ Y_w \\ Z_w \end{pmatrix} + \boldsymbol{t} $$ を同次座標で表現すると, $$ \tilde{\boldsymbol{X}} \sim \boldsymbol{M} \tilde{\boldsymbol{X_w}} $$ ここで, $$ \begin{align} \boldsymbol{M} \sim \begin{pmatrix} \boldsymbol{R} &\boldsymbol{t} \\ 0^T &1 \end{pmatrix} &= \begin{pmatrix} r_{11} &r_{12} &r_{13} &t_1 \\ r_{21} &r_{22} &r_{23} &t_2 \\ r_{31} &r_{32} &r_{33} &t_3 \\ 0 &0 &0 &1 \end{pmatrix} \end{align} $$

画像座標と正規化画像座標の関係

$$\tilde{\boldsymbol{m}} \sim \boldsymbol{A}\tilde{\boldsymbol{x}}$$ ただし、 $\boldsymbol{A}$ は以下のようなカメラ内部パラメータからなる 3x3 の行列である. $$ \boldsymbol{A} = \begin{pmatrix} \frac{f}{\delta_u} &0 &c_u \\ 0 &\frac{f}{\delta_v} &c_v \\ 0 &0 &1 \end{pmatrix} $$

ワールド座標系と画像座標の関係

$$ \begin{align} \tilde{\boldsymbol{m}} &\sim \boldsymbol{A}\tilde{\boldsymbol{x}} \\ &\sim \boldsymbol{A}(\boldsymbol{I}|0) \tilde{\boldsymbol{X}} \\ &\sim \boldsymbol{A}(\boldsymbol{I}|0) \begin{pmatrix} \boldsymbol{R} &\boldsymbol{t} \\ 0^T &1 \end{pmatrix} \tilde{\boldsymbol{X_w}} \\ &\sim \boldsymbol{A}(\boldsymbol{R}|\boldsymbol{t}) \tilde{\boldsymbol{X_w}} \end{align} $$

ここで, 透視変換行列（カメラ行列） $\boldsymbol{P} = \boldsymbol{A}(\boldsymbol{R}|\boldsymbol{t})$ とすると,

$$ \tilde{\boldsymbol{m}} \sim \boldsymbol{P} \tilde{\boldsymbol{X_w}} $$

という簡単な式で表現できる.

参考文献

ディジタル画像処理[改訂新版]

2019-01-11

ワールド座標系の基礎 1

ComputerVision

この記事では, ワールド座標系について解説します. 仕事で扱うことがあるので理解を深めるためにまとめてみました.

画像の幾何学的モデル

ここでは, 理想的な条件においてモデルの概念説明を行う.

ピンホールカメラモデル

ピンホール位置（光学中心）を原点とする3次元空間の座標を $(X, Y, Z)$ , $Z = -f$ の平面を投影面, 投影面上の画像中心を原点とする座標画像を $(x, y)$ とする.

f:id:nekketsu-engineer:20190110072210p:plain

この時, 物体の高さ $Y$ と投影面上にできる画像の大きさ $y$ との関係は, $Y:Z=y:f$ である. 同様に考えると, $(x,y)$ は $$x=-f\frac{X}{Z}$$ $$y=-f\frac{Y}{Z}$$ となる.

透視投影モデル

ピンホールモデルの場合, 上下左右反転となるため取り扱いが煩わしいため, コンピュータービジョンでは透視投影モデルを利用する. 透視投影モデルでは, 光学中心よりも後方のピンホールで反転した像を取り扱うのではなく, 光学中心よりも焦点距離分だけ物体側に仮想投影面を置き, そこに反転していない像を描画するモデルである.

f:id:nekketsu-engineer:20190110072231p:plain

前述の定義より自明であるが, $(x,y)$ は $$x=f\frac{X}{Z}$$ $$y=f\frac{Y}{Z}$$ となる.

画像と空間の幾何学的関係

座標系 (CS; coordinate system) 概要

名称	概要
画像座標系 (image CS)	ピクセル単位のカメラ画像
正規化画像座標系 (normalized image CS)	その名の通り, 画像座標系（pixel単位, 画像左上が原点）を正規化して実距離空間で扱えるようにした座標系（mm単位, 画像の中心が原点）. 正規化の際に, レンズ光軸と画像座標系中心のずれ, 座標原点の変換, 仮想平面への距離を $f=1$ （カメラ座標系における $Z=1$ [mm] ）に規格化する. 正規化画像座標で表現することで, その後の座標変換をすべてピンホールモデルで扱えるようになる. 画像中心とレンズ光軸中心が一致し直交する.
カメラ座標系 (camera CS)	カメラの光学中心を原点とし, Z軸をカメラの光軸方向に一致させ, X軸とY軸は画像の横方向と縦方向に平行にとった座標系.
ワールド座標系 (world CS)	カメラ座標とは独立の任意の座標系. $Y_w=0$ の平面像を鳥瞰図という. WCSから鳥瞰図に変換する際には, 3Dから2Dへの透視変換が必要.

f:id:nekketsu-engineer:20190110072246p:plain

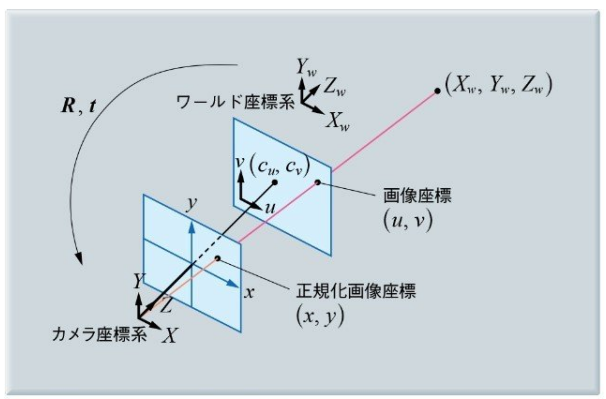
絵の説明:

正規化画像座標系は
- カメラ座標系の Z 軸と画像中心が一致する.
- 焦点距離は $f= 1$ が仮定されている.
カメラ座標系の Z 軸と画像座標系の中心は一致しない（カメラ中心と光学中心はずれている）

正規化画像座標系とワールド座標の関係式

正規化画像座標系とカメラ座標の関係

カメラ座標系の空間位置 $(X, Y, Z)$ と正規化画像上の位置 $(x, y)$ には, 以下の関係が成り立つ. これは, ピンホールカメラモデルと透視投影モデルの組み合わせである. $$x = \frac{X}{Z}$$ $$y = \frac{Y}{Z}$$

カメラ座標系とワールド座標系の関係

空間中のある任意な位置に任意の方向で存在するワールド座標系を考える. ワールド座標系における任意の空間の点を $(X_w, Y_w, Z_w)$ とし, 同じ点をカメラ座標系で表した位置 $(X, Y, Z)$ との関係を定式化すると,

$$ \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} = \boldsymbol{R} \begin{pmatrix} X_w \\ Y_w \\ Z_w \end{pmatrix} + \boldsymbol{t} $$

ここで, $\boldsymbol{R}$ , $\boldsymbol{t}$ はワールド座標系を画像座標系に変換する回転行列(3x3)と平行移動ベクトル（カメラ座標から見たワールド座標系原点の位置）である.

$$ \boldsymbol{R} = \begin{pmatrix} r_{11} & r_{12} &r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{pmatrix} $$ $$ \boldsymbol{t} = \begin{pmatrix} t_1 \\ t_2 \\ t_3 \end{pmatrix} $$

回転行列について: 回転の順序によりマトリックスが異なる点に注意.
ここでは, ある点が $X$ 軸周りに角度 $\alpha$ , $Y$ 軸周りに角度 $\beta$ , $Z$ 軸周りに角度 $\gamma$ と, 順に回転する場合を考える. 回転行列は,

$$ \begin{align} \boldsymbol{R} &= \boldsymbol{R_Z} \cdot \boldsymbol{R_Y} \cdot \boldsymbol{R_X} \\ &= \begin{pmatrix} \cos{\gamma} &-\sin{\gamma} &0 \\ \sin{\gamma} &\cos{\gamma} &0\\ 0 &0 &1 \end{pmatrix} \begin{pmatrix} \cos{\beta} &0 &\sin{\beta} \\ 0 &1 &0\\ -\sin{\beta} &0 &\cos{\beta} \end{pmatrix} \begin{pmatrix} 1 &0 &0 \\ 0 &\cos{\alpha} &-\sin{\alpha}\\ 0 &\sin{\alpha} &\cos{\alpha} \end{pmatrix} \\ &= \begin{pmatrix} cos{\beta}\cos{\gamma} &-\cos{\alpha}\sin{\gamma}+\sin{\alpha}\sin{\beta}\cos{\gamma} &\sin{\alpha}\sin{\gamma}+\cos{\alpha}\sin{\beta}\cos{\gamma} \\ \cos{\beta}\sin{\gamma} &\cos{\alpha}\cos{\gamma}+\sin{\alpha}\sin{\beta}\sin{\gamma} &-\sin{\alpha}\cos{\gamma}+\cos{\alpha}\sin{\beta}\sin{\gamma}\\ \sin{\beta} &\sin{\alpha}\cos{\beta} &\cos{\alpha}\cos{\beta} \end{pmatrix} \end{align} $$

画像座標系と正規化画像座標の関係

画像座標を $(u, v)$ とする. 正規化画像座標は, これまでの説明通り $(x, y)$ とする. 画像座標系と正規化画像を紐づける以下のパラメータを定義する.

パラメータ名	記号	単位
カメラ焦点距離	$f$	mm
カメラ画素横方向サイズ	$\delta{u}$	mm
カメラ画素縦方向サイズ	$\delta{v}$	mm
画像座標系における光軸と画像面（投影面）との交点の横方向位置	$c_u$	pixel
画像座標系における光軸と画像面（投影面）との交点の縦方向位置	$c_v$	pixel

画像座標系における光軸と画像面（投影面）との交点を画像中心と呼ぶ.
CCD の物理的な配置により, 光軸との交点が必ずしも CCD の中心と一致しないため, ここでいう画像中心は, 入力画像の中心に位置するとは限らない.
厳密には CCD と光軸が完全には直交しないが, 無視できるほど小さいとみなす.

上記パラメータを使って画像座標系と正規化画像座標系の関係式を表すと, $$x=\frac{\delta_u(u-c_u)}{f}$$ $$y=\frac{\delta_v(v-c_v)}{f}$$

参考文献

ディジタル画像処理[改訂新版]

2018-12-10

言語仕様の違いをまとめてみた

プログラミング全般

C, C++, C#, Python の言語仕様の違いをなんとなくまとめてみました.
というのも, Udacity のコース内で Python → C++ を学習するという流れの説明の際に Syntax は慣れた言語と比較して覚えると良いとの助言があり, 確かに！と思ったからです. この記事では, C, C++, C#, Python で言語ごとに仕様が異なる部分についてまとめます.

ライブラリ

C / C++

#include <libraryname>

主にヘッダーファイル
<libraryname> で記載すると, 標準ライブラリを想定. コンパイラオプションや環境変数で指定されるパスを優先して検索.
"libraryname" で記載すると, ソースファイルのあるパスを優先して検索.

C＃

コンパイラに DLL を指定してコンパイル.
Visual Studio の場合は参照を追加する.

Python:

import modulename
import packagename.modulename
from packagename import modulename

モジュール
- 関数ライブラリのようなもの.
- モジュール内スコープで有効なグローバルな変数を定義可. モジュール外からは modulename.variablename でアクセスも可能（非推奨）.
- ファイル単位で１つのモジュールとなる.
パッケージ
- クラスライブラリのようなもの.
- パッケージ内に複数のモジュールを持つ.
- ファイル単位で１つのパッケージとなる.
- あるディレクトリをパッケージが存在するディレクトリとして認識させるためには __init__.py ファイルを置く必要がある.

名前空間 / スコープ / アクセス修飾 etc.

C

名前空間 / スコープ

ブロックスコープ
- ブロック内のみ有効.
ローカルスコープ
- ローカル変数. スコープは関数内に限定.
ファイルスコープ
- グローバル変数.
- 普通ではファイル内にスコープは限定される.
- ただし, extern をつけて同じ名前で宣言すれば他のファイルからも参照できる.
静的変数
- プログラム開始から終了まで 1 つのオブジェクトとして記憶される.
- static をつけて宣言する.
- 確実にファイル内のみにスコープが限定される.

アクセス修飾

N/A

C++

名前空間 / スコープ

ブロックスコープ
- ブロック内のみ有効.
ローカルスコープ
- ローカル変数. スコープは関数内に限定.
クラススコープ
- クラスメンバ
- インスタンスメンバ
ファイルスコープ（名前空間スコープ）
- グローバル変数.
- 普通ではファイル内にスコープは限定される.
- ::variable とスコープ演算子を使うと, 他のファイルからも参照できる.
名前空間
- ファイル単位で名前空間を形成する.
- 参照方法

/*
--- １ ---
using ディレクティブ.
ファイル冒頭かクラス内または関数内に配置できる.
名前空間以下の全てにダイレクトアクセスできるようになる
*/
using namespace Something; // Something 名前空間の全てにアクセス可
A objectA;
objectA.Dosomthing();
B objectB;
objectB.Dosomthing();

/*
--- 2 ---
using ディレクティブ.
名前空間のある機能のみにアクセス
*/
using namespace Something::A; // Something 内の A クラスにアクセス
A objectname;
objectname.Dosomthing();

/*
--- 3 ---
完全修飾. 都度 namespace 付きでアクセス.
*/
std::cout << "XXXX" << "\n" // 完全修飾で std 名前空間の cout 関数にアクセス

クラススコープ
- クラスメンバー変数. スコープはクラス内に限定.
- クラス外からは, 変数の場合 InstanceName.Variable / ポインタ変数の場合 InstanceName->Variable としてアクセスできる.

アクセス修飾

public
- 変数/関数はクラス外からアクセス可能.
- public レベルで継承した場合, 基底クラスの public メンバは派生クラスの public メンバとなる.
private
- 変数/関数はクラス外からのアクセス禁止.
- private レベルで継承した場合, 基底クラスの public メンバが派生クラスの private メンバとなる.
protected
- 変数/関数はクラス外からアクセス禁止. private のように振る舞う.
- protected レベルで継承した場合, private メンバーも派生クラスからはアクセス可能.

C＃

名前空間 / スコープ

C++ と同様
クラス定義は partial をつければファイルを跨げる
名前空間はファイルを跨げる
名前空間の利用法は同じ.
名前空間は階層構造を持てる.

// using ディレクティブ
using System;

// 完全修飾.
x = System.Drawing.Image

アクセス修飾

C++ と同様.

Python

名前空間 / スコープ

基本的には他の言語と同じ.
クラス変数, 他の言語でいう static メンバ変数.

# x はクラス変数
class SomeClass():
      x = 5
      def somothing():
        ....

インスタンス変数

# x はインスタンス変数
class SomeClass():
      def __init__(self):
        self.x = 5
      def somothing():
        ....

モジュール, パッケージ共に import で参照できる.

アクセス修飾

基本的に public となる.
private にしたい場合は __variable / __function() と接頭にアンダーバー2つを付けて宣言する.

オーバーロード

C	C++	C#	Python
不可	可	可	不可

標準入出力

C

int x;
scanf("%d", &x); // アドレス指定
printf("値は x = %d です.", x); // 変数指定

C++

int x;
std::cin >> x; // 変数指定
std::cout << "値は x = " << x << "です." << "\n" //変数指定

C＃

int x  = Console.ReadLine(); // etc.
Consolr.WriteLine("値は x = {0} です.", x)

Python

x = input()
print("値は x = %d です." % x)
print("値は x = {0} です.".format(x))

論理演算

	C	C++	C#	Python
AND	&&	&&	&&	and
OR	\|\|	\|\|	\|\|	or
NOT	!	!	!	not

2018-07-22

論理演算表記のまとめ

数学

背景

現在、Udacity の Artificial Intelligence Nanodegree を受講しているのですが、その中で初めて A AND B を数理論理学では $A \land B$ と書くことを知りました。高校数学等でベン図を使って理解する時には $A \cap B$ で習っていたし、最近は AND, OR, XOR という表記でしか書かないので混乱することがあるため、理解のために様々な表記法をまとめる記事を書こうと思いました。